ポワソン分布

今日は「ポワソン分布」について解説します。スポーツアナリティクスではよく使われる統計モデルのひとつですが、統計学の勉強を始めたばかりだと、理解があやふやな方も多いかもしれませんね。

確かに名前は聞いたことがあるような気がしますが、きちんと理解できていないかもしれません。

簡単に言うと、「ある一定の時間や空間で、まれに起こる出来事の回数を表す確率分布」です。たとえば「野球で3打席連続でホームランを打つ確率」、さらに「サッカーの1試合での得点数」などを扱うときによく使われます。

特徴は次の2つです。

特徴➀：平均（λ）が決まれば、分布の形が決まる
特徴②：分布の形をもとに、「発生回数が0回」、「1回」、「2回…」といった「まれに起こる出来事」の発生確率を計算できる

なるほど。具体的にどうやって計算するんですか？

ポワソン分布の確率は次の式で表されます。

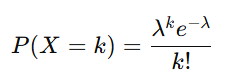
ここで

●λ（ラムダ）：平均発生回数（例えば、サッカーでクラブAは1試合で平均1.2得点など）
●k：実際に起きた回数（0点、1点、2点…、を取った回数）

つまり「平均1.2点取るチームが、この試合で2点取る確率は？」といった問いに答えられるんです。

なんとなくわかったような、わからないような…。スポーツにどう役立つんですか？

スポーツアナリティクスでは、大きく3つの活用法が考えられます。

１：試合結果予測
サッカーの得点数はポワソン分布に従いやすいことが知られています。両チームの平均得点をもとに「0-0の確率」「1-0の確率」などを計算できます。これにより、引き分けや勝敗の確率を推定できます。

２：選手パフォーマンスの評価
バスケの3ポイント成功数、野球の本塁打数など、「まれに起きる成功イベント」を確率モデルとして捉えることができます。その結果、5打席連続でホームランを打った選手でいかに凄いか、シーズンを24勝0敗で終えた投手がどれほど優秀なのかを確率で表現することができます。

３：戦術や意思決定への応用
例えばPK戦での得点確率を選手ごとに推定したり、交代選手を投入したときの得点期待値をモデル化したりする際に使えます 。「勘と経験」の采配から脱却でき、データドリブンな戦術実行が可能になります。

スポーツのあらゆるシーンにおいて活用できるのですね。「確率が描くJ1最終盤のシナリオ —— 勝ち点期待値から読み解く優勝争い」を読みました。この記事では、具体的にポワソン分布をどう使っているんですか？

大枠は次の3ステップです。
ポワソン分布で1試合の得点分布を出し、その分布からスコア別確率、さらに勝ち点期待値を計算して、残り全試合に適用しています。

Step 1：λ（平均得点）/ λ（平均失点）の推定
各クラブの平均得点・失点をベースに、直近10試合の勢い、残り試合の相手の強さ（順位）、過去の相性で補正して、対戦カードごとの期待得点・期待失点を作ります。

Step 2：スコア別確率
ホーム/アウェイ各チームのλを使い、ポワソン分布で「0〜4点を取る確率」を計算。両チームを掛け合わせてスコア表（0-0, 1-0, 1-1…）を作ります。

Step 3：勝ち点期待値
そのスコア表から勝率・引分率・敗率を集計し、3×勝率 + 1×引分率で1試合の勝ち点期待値を出し、残り全試合分を合計します。

記事中の「京都vsセレッソ」の図は、この手順で出しているわけですね？

その通りです！京都の攻撃力・守備力に、相手であるセレッソの強さや直近の勢い・相性の補正を掛けて λ を作成。そこからスコア別確率を出すと、記事では「2-1で京都勝利」9.5％、「1-1」8.6％、「2-0」7.2％といった並びになりました。スコア範囲を広げれば、勝率・引分率・敗率も同じ表から算出できます。

1カードの確率が出たとして、優勝争いの見通しはどうやって作ったんですか？

各クラブの残り全試合について同じ計算を行い、勝ち点期待値を積み上げます。
例えば京都は「残り11試合で20.3ポイントを獲得」と見積もられ、最終勝点は71.3（≒71）となりました。全20クラブで同様に求めると、記事の結論通り、鹿島72.2、京都71.3という拮抗した優勝レースのシナリオが描けます。

「勢い」や「相性」って、モデルの中ではどう反映しているんですか？

λの倍率補正として入れています。直近10試合の得失点傾向で攻撃/守備の強度を微調整し、対戦相手の順位や直接対戦成績（相性）でさらに上げ下げするイメージです。こうすることで、単純な通期平均よりも現実に近いスコア確率になります。

なるほど！ じゃあ、この予測は「当たり・外れ」を競うというより、可能性の地図を示す感じですね。

まさにそれです。選手の負傷や退場、偶然のワンプレーは織り込めませんが、「平均的にこう転びやすい」を数値化できます。だからこそ、残りカードの重さ（相手の強さや相性）が勝ち点にどう効くかを透明化でき、記事では鹿島がわずかに優位という結論につながりました。

よく分かりました。ポワソン分布が、試合単位の確率からシーズンの見通しまでつながるんですね！